Óptica Geométrica: 23. Estudo Analítico das Lentes

Equação de Gauss

Observe o esquema abaixo:

Onde:

f = distância focal

p = distância do objeto ao centro óptico da lente

p' = distância da imagem ao centro óptico da lente

hₒ= altura do objeto

hᵢ = altura da imagem

As três primeira medidas estão relacionadas pela seguinte equação:

A chamada Equação de Gauss, a mesma que usamos para os espelhos esféricos.

Aumento Linear Transversal (A)

As duas últimas medidas definem o aumento linear transversal, como também já vimos nos espelhos esféricos:

Que também pode ser definido assim:

Em alguns problemas, é importante usar o seguinte resultado em relação ao aumento:

Mas, para usarmos a Equação de Gauss e o aumento em qualquer situação, precisamos considerar a seguinte convenção de sinais:

f > 0 (positivo)→ lente convergente;

f < 0 (negativo)→ lente divergente;

P > 0 (positivo)→ objeto real;

P < 0 (negativo)→ objeto virtual

(Uma imagem real de uma lente pode servir de objeto virtual para uma segunda lente);

P’> 0 (positivo)→ imagem real;

P’ < 0 (negativo)→ imagem virtual;

hₒ > 0 (positivo)→ objeto para cima

hₒ < 0 (negativo)→ objeto para baixo

hᵢ > 0 (positivo)→ imagem para cima;

hᵢ < 0 (negativo)→ imagem para baixo;

Exemplo 1:

Um objeto está a 30cm de uma lente esférica convergente que tem distância focal f=20cm.

a) Faça um esboço para representar a formação da imagem.

b) A que distância a imagem está da lente?

Resolução:

b) O objetivo é determinar a distância da imagem à lente, ou seja, p'. Caso soubéssemos qual o valor do aumento (A) poderíamos encontrar p', mas não foi informado. Só nos resta a Equação de Gauss.

Como a lente é convergente, f>o, logo f=20cm. Assim:

Caso tenha dificuldades com operações entre frações, você pode usar números decimais. Lembre-se de usar o número de algarismos significativos coerentes no calculo!

Percebe que o valor encontrado é um pouco diferente daquele calculado quando usamos as frações. É que quando transformamos frações em números decimais, é comum obtermos dízimas. Essas dízimas precisam ser aproximadas para que tenham um certo número de algarismos significativos. Essas aproximações geram pequenos erros que se propagam durante o cálculo.

Exemplo 2

Um objeto com 15cm de altura está diante de uma lente esférica divergente que tem distância focal f=-20cm. A respectiva imagem tem altura de 5,0cm.

a) Faça um esboço para representar a formação da imagem.

b) Qual o aumento linear transversal?

c) A que distância o objeto está da lente?

Resolução:

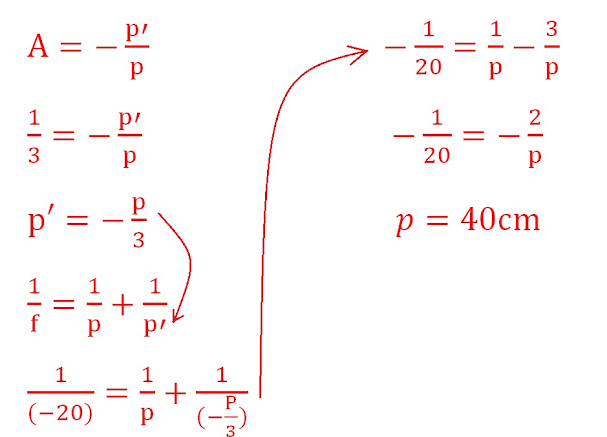
b) Como o objeto e a imagem estão para cima, ambos são positivos, assim:

Esse resultado significa que a imagem tem 1/3 da altura do objeto.

→Clique aqui para continuar.